728x90
부분집합?
부분집합이란 집합에 포함된 원소들을 선택하는 것이다.
부분집합의 수
- 집합의 원소가 n개일 때, 공집합을 포함한 부분집합의 수는 2ⁿ개다.
- 이는 각 원소를 부분집합에 포함시키거나 포함시키지 않은 2가지 경우를 모든 원소에 적용한 경우의 수와 같다.
- 예) {1,2,3,4} => 2*2*2*2 = 16가지
부분집합 구현 - 반복문
코드

결과

부분집합 구현 - 재귀
코드

결과

부분집합 응용 - 바이너리 카운팅
바이너리 카운팅을 통한 사전적 순서(Lexicographical Order)로 생성하는 방법
바이너리 카운팅(Binary Counting)은 사전적 순서로 생성하기 위한 가장 간단한 방법
원소 수에 해당하는 N개의 비트열을 이용하며, N번째 비트값이 1이면 n번째 원소가 포함되었음을 의미함
부분집합 구현 - 바이너리 카운팅
코드

결과
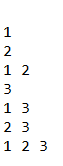
전체 코드
더보기
public class Main {
static int N = 3;
static int[] input = {1, 2, 3};
static int[] selected = new int[N];
static void subset_for() {
// selected에 1이 들어있으면 선택한 것. 0이면 선택 안한 것.
for(int i = 1; i >= 0; i--) {
selected[0] = i; // 원소 1
for(int j = 1; j >= 0; j--) {
selected[1] = j; // 원소 2
for(int k = 1; k >= 0; k--) {
selected[2] = k; // 원소 3
for(int m = 0; m < 3; m++) {
if(selected[m] == 1) { // 생성된 부분집합 출력
System.out.print(input[m] + " ");
}
}
System.out.println();
}
}
}
}
static boolean[] isSelected = new boolean[N]; // 사용한 숫자인지 확인하는 배열
static void subset_recursive(int cnt) { // cnt: 현재까지 처리한 원소 갯수
if(cnt == N) {
for(int i = 0; i < N; i++) {
if(isSelected[i]) {
System.out.print(input[i] + " ");
}
}
System.out.println();
return;
}
isSelected[cnt] = true;
subset_recursive(cnt + 1);
isSelected[cnt] = false;
subset_recursive(cnt + 1);
}
static void subset_binary() {
for(int i = 0; i < (1 << N); i++) { // 1 << n: 부분집합의 갯수
for(int j = 0; j < N; j++) { // 원소의 수만큼 비트를 비교함
if((i & (1<<j)) != 0) { // i의 j번째 비트가 1이면 번째 원소를 출력
System.out.print(input[j] + " ");
}
}
System.out.println();
}
}
public static void main(String[] args) {
subset_for();
System.out.println();
subset_recursive(0);
System.out.println();
subset_binary();
}
}728x90
'개발 > 알고리즘' 카테고리의 다른 글
| 중복 순열, 순열, 중복 조합, 조합 (0) | 2023.08.12 |
|---|---|
| 조합(Combination) (0) | 2023.08.12 |
| 순열(Permutation) (0) | 2023.08.12 |
| 완전 검색, 완전 탐색(Exhaustive Search) (0) | 2023.08.12 |